Have you solved the simple version and the challenge version? Now, the ultimate version is coming :]. The difference between this version and the challenge version is:
the element of range from [start,end] into [start,end,num]That is, before we calculate the sum value, we need to replace the element with
numat the start index.Task
Given an array
arrthat contains some integers(positive, negative or 0), and arangelist such as[[start1,end1,num1],[start2,end2,num2],...], start and end are the index ofarrand start always less than end. Your task is replace the value of arr[start] withnum, and then calculte the sum value of each range (start index and end index are both inclusive), and return the maximum sum value.For example:
Given arr = [1,-2,3,4,-5,-4,3,2,1], range = [[1,3,5],[0,4,2],[6,8,1]] should return 12 calculte process: step 1: replace arr[1] with 5 then arr = [1,5,3,4,-5,-4,3,2,1] range[1,3] = arr[1]+arr[2]+arr[3] = 5 + 3 + 4 = 12 step 2: replace arr[0] with 2 then arr = [2,5,3,4,-5,-4,3,2,1] range[0,4] = arr[0]+arr[1]+arr[2]+arr[3]+arr[4] = 2 + 5 + 3 + 4 + -5 = 9 step 3: replace arr[6] with 1 then arr = [2,5,3,4,-5,-4,1,2,1] range[6,8] = arr[6]+arr[7]+arr[8] = 1 + 2 + 1 = 4 So the maximum sum value is 12Note:
arralways has at least 5 elements;rangealways has at least 1 elements;- The replacement operation is carried out step by step, according to the order of range. The replacement operations will affect the results of the calculations, please be careful 😉
- All inputs are valid;
- This is a ultimate version, Please optimize your algorithm to avoid time out 😉
- If you feel difficult, please try the simple version or try the challenge version.
About testcases
- Basic test: 3 testcases
- Random test1: 100 testcases
- each arr : 5-100 elements
- each range : 1-6 elements
- Random test2: 100 testcases
- each arr : 100000 elements
- each range : 10000 elements
Some Examples
CodewarsmaxSum([1,-2,3,4,-5,-4,3,2,1],[[1,3,5],[0,4,2],[6,8,1]]) === 12 maxSum([1,-2,3,4,-5,-4,3,2,1],[[1,3,10]]) === 17 maxSum([1,-2,3,4,-5,-4,3,2,1],[[1,4,6],[2,5,4]]) === 8
Brute Force
procedure maxSum(arr, range) // range is multidimensional array
1. set sum to -Infinity
2. for i equals 0 to range.length
A. set r to range[i]
B. arr[r[0]] = r[2]
C. set temp to 0
D. for j equlas 0 to arr.slice(r[0], r[1] + 1) // start, end
I. temp += arr[j]
E. if temp > sum then sum = temp
3. return sum
The runtime complexity of this algorithm is quadratic – O(ra), where r is the array of ranges and a is the array.
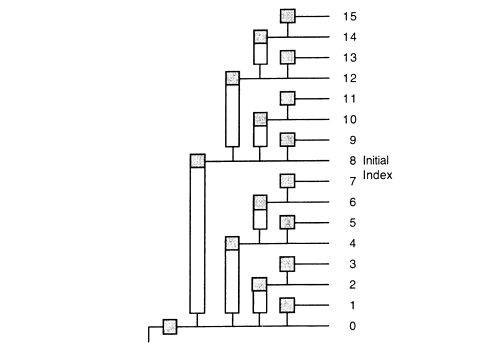
By implementing fenwick tree we can improve the runtime of this algorithm to run at O(Rlog A[start], A[end]:A), in which the upper bound is much closer to linear time – O(Rlog A[start], A[end]:A) = O(log n + n) = O(n).
Using Binary Indexed Tree
procedure maxSum(arr, range)
1. set tree to arr
2. for i equals 0 to arr.length // the upper bound O(n)
A. set j to bit representation of i
B. if j < arr.length then tree[j] += tree[i];
3. set max to -Infinity
4. for each start, end, num in range // O(n)
A. set i to start, v to num - arr[start], n to arr.length, sum to 0
B. while i < n // O(log n)
I. tree[i] += v
II. assign to i itself + 1 binary representtional value
C. i = end
D. while i >= start && i <= end // O(log n)
I. sum += tree[i]
II. i equals i and i+1 binary representation
III. i--
E. if sum > max then max = sum
5. return max